
Microsoft has the point at h/w*p, meaning that the proportion will only be valid if the w/h-ratio is 1, which it isn't, it's 2/sqr(3). So one thinks the Adjustments(1), which is the point where Microsoft determines where to put the corner point, for the hexagon should be 0.25, but no. The first corner, the top left one, is at 25% of the width. 28706, and lo and behold, that was the magic number.Ī regular hexagon has a width-to-height ratio of 2/sqr(3). 28002, and my many attempts to get it right with none of them working, I tried taking half of. Given the starting value of the close-but-not-quite hexagon of.

Then I tried setting it as far right (turning the hexagon into a diamond) and got. So I set it to the furthest left it could go (turning the hexagon into a square) and the value was 0.
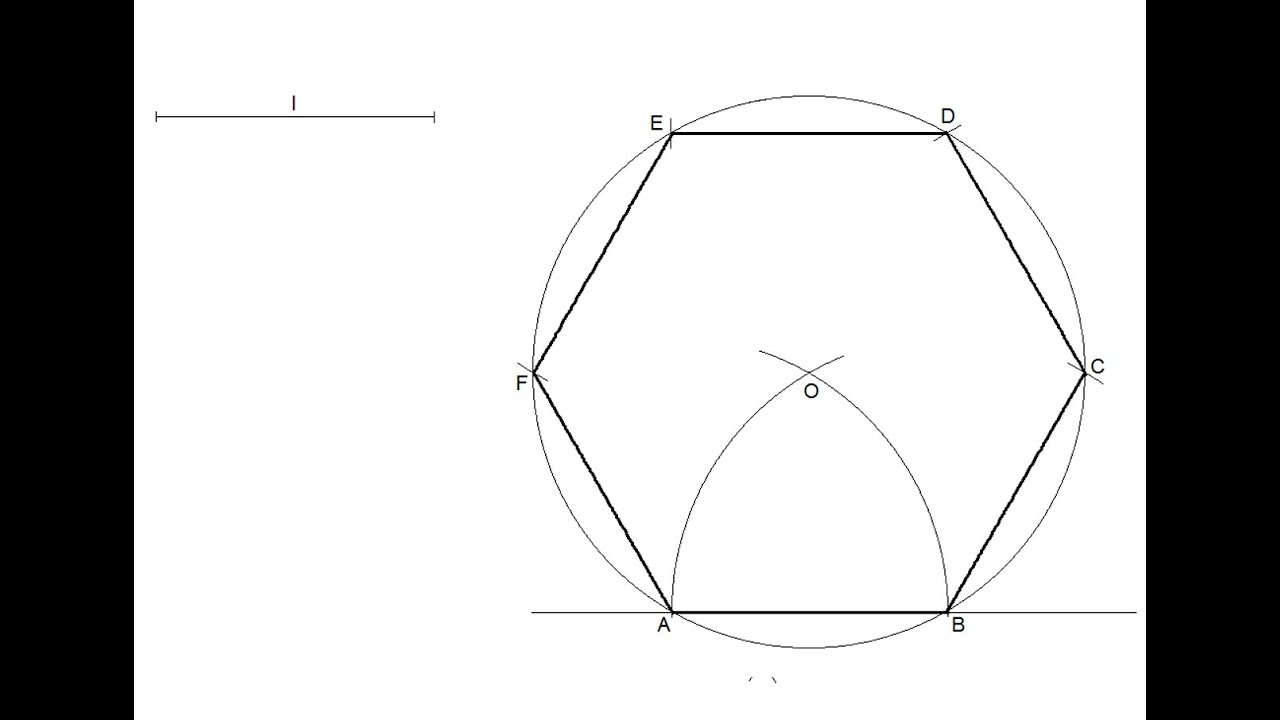
28002, so I started fiddling around and trying to do math assuming that this value was somehow based on angles. The value for the close-but-not-quite hexagon was. I used some VBA to check what the position of the handle was (with the hexagon selected): ?(1).Adjustments(1) So, the measure of the sixth angle is 170°.To get a regular hexagon in PowerPoint, create a hexagon using shift, then run the following VBA command with that hexagon selected: (1).Adjustments(1) = 0.28706Īfter I created the approximate shape using the overlay on the close-but-not-quite equilateral triangle, I decided to get programmatic. Sum of the interior angles in hexagon = 720° What is the length of its sides?Įxample 3: Five angles of a hexagon measure 110° each. So, the perimeter of the hexagon is 120 cm.Įxample 2: The perimeter of a regular hexagon is 36 cm. Perimeter of regular hexagon = 6 × length of side Perimeter = a + a + a + a + a + a = 6 a Solved Examples on HexagonĮxample 1: Find the perimeter of a regular hexagon having each side measure 20 cm. So, the perimeter of a regular hexagon is six times the length of one side. In regular hexagons, all sides are equal in length. The perimeter of a hexagon is the sum of the length of all 6 sides.

Concave Hexagonįor concave hexagons, at least one of its interior angles must be greater than 180° and at least one of its vertex points inwards. Convex hexagons can be regular or irregular. Convex Hexagonįor convex hexagons, all of its interior angles must be less than 180 degrees, and all the vertices are pointed outwards. Classification of hexagons based on their angles 1.


 0 kommentar(er)
0 kommentar(er)
